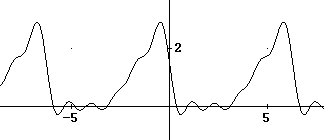
es de la forma SERIE DE FOURIER
La serie de Fourier de funciones de período
es de la forma
donde los coeficientes están dados por
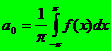
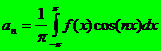
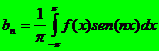
La serie converge a
si la misma es continua. Si
es seccionalmente continua, el valor de la serie es la
semisuma de los límites laterales en los cuales la función presenta la
discontinuidad. Además deben existir las derivadas laterales deen cada punto del intervalo.
EJEMPLO 1)
Desarrollar en serie de Fourier
Calculamos los coeficientes
Para
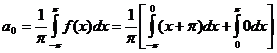
Para 
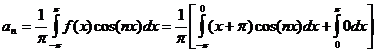
Integrando por partes la primera integral encerrada entre corchetes, obtenemos
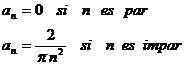
Para 
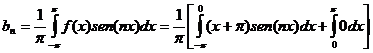
Nuevamente integrando por partes, resulta
Luego siendo la serie de Fourier
resulta para los puntos en que la función es continua
La función es discontinua en
, dentro del intervalo de periodicidad; por lo tanto la serie
toma el valor 
en ese punto (ya
que es la semisuma de los límites laterales de la función) y en cualquier otro punto en donde se presenta la discontinuidad.
La gráfica aproximada es
