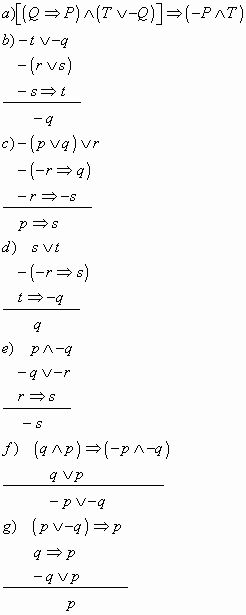
Matemática Discreta
1 Determinar la validez de:
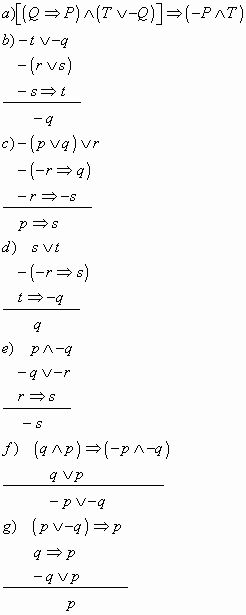
2 Determinar si es tautalogía: 
3 Dada la siguiente proposición compuesta y sabiendo que q es falsa decidir los valores de verdad que tomaría dicha proposición:
4 Dadas las proposiciones p, q, r construya con ellas una proposición compuesta y luego determine si es tautología.
5 Si : 
calcular: 
6 Determine los conjuntos A y B sabiendo que: 
7 Graficar : 
8 Proponer dos conjuntos A y B finitos cuya unión sea: 
,
la intersección vacía y la diferencia A-B resulte ser: 
9 Determinar si se cumple: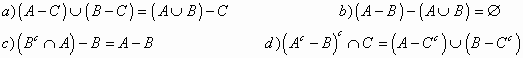 
10 Dar forma explícita y recursiva de 2, -4, 8, -16, 32,.........
4, -2, 1, -
, 
,..........
11 Se arrojan 4 dados de 6 caras numerados del 1 al 6. ¿ De cúantas formas distintas pueden salir, suponiendo que no pueden salir dos números iguales en dos dados distintos en un misma tirada?
12 Con los dígitos 1, 2, 3, 4, 5 ¿ Cuántos números de 3 cifras distintas se pueden formar, si dichos números deben comenzar con el 3 y deben ser impares?
13 Con los dígitos 0, 1, 2, 3, 4 determinar la cantidad de números impares de tres cifras distintas que existen.
14 ¿Cuántos números pares de tres cifras distintas pueden formarse con : 1, 3, 5, 4, 6?
15 ¿Cuántos números pares de cifras distintas que sean menores de 3000 pueden formarse con los dígitos: 0, 1, 2, 3, 4, 5, 6, 8?
16 Probar por inducción completa:
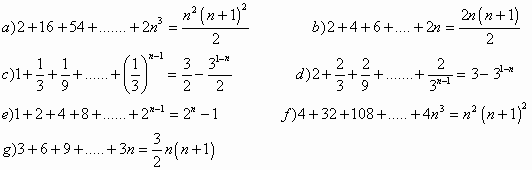
17 Hallar t y s enteros tales que: 
18) Sea la relación
.
Se pide
a) dominio de R; b) imagen de R; c) matriz de la relación; d) dígrafo; e) grados externos e internos. f) Clasificación, justificando cada propiedad;
g) efectuar las cerraduras reflexiva, simétrica (¿es necesaria?) y transitiva (por el algoritmo de Warshall)
19) Sea
definidas en 
.
Hallar
20) Hallar si existen
si 
21) ¿Es posible determinar la función
inversa de 
? Justifique su respuesta. En caso afirmativo, hállela.
22) Encuentre
si 
son permutaciones definidas en
23) Encuentre el orden del producto de
ciclos 
. Determine la paridad de la permutación obtenida si
