Álgebra Aplicada

Sucesiones    Combinatoria    Vectores    Matrices   

Determinantes   Sistema de ecuaciones e inecuaciones

Sucesiones

1) Escriba los 5 primero términos de las siguientes sucesiones

a) n/2      b) 4n-1        c) (n+5)/(n+3)        d) (-1)ⁿ n / 4         e) nⁿ⁺²

2) Escriba la fórmula correspondiente

a) 1/3, 1/6, 1/9, 1/12, . . .          b) -1, 4, -9, 16, . . .          c) 1, 4, 27, . . .

3) En una sucesión aritmética de razón 1/3 el primer término es 8, calcular el quinto y la suma de todos ellos.

4) Calcular el número de términos de una sucesión aritmética si a₁=2 ,  r =5 y el último término 97

5) Interpolar tres términos entre 3/4 y 5/2 para que resulte una suesión aritmética.

6) La suma de tres términos consecutivos de una sucesión aritmética es 18 y la suma de sus cuadrados es 116. ¿Cuáles son los números?.

7) Hallar el valor de k  para que la sucesión  2k+1, 4k-3, k+8 resulte aritmética.

8) Para que valor de n se cumple 2+5+8+. . . >610

9) Calcular el décimo término de la sucesión 4, 12, 36, ... y la suma de todos ellos.

10) Interpolar en sucesión geométrica 4 términos entre 5  y  -1215

11) El producto entre el primer y el tercer término de una sucesión geométrica es 1/9 y el cociente entre el primero y el quinto es 81. Calcularlos.

12) En una sucesión geométrica de razón 3, la suma de los n primeros términos es 728. Hallar n y a_n sabiendo que el primer término es 2

Combinatoria

1) Calcular

a)  14! / 12!      b)  (n+1)! / n!     c) (n-1)! / (n-2)!

2) Cuántos números de 4 cifras distintas pueden formarse con los dígitos 3, 4, 6, 8, 9

3) Cuantos triángulos se forman con un polígono de 7 lados.

4) Una escuela solicita cubrir los cargos de director, vicedirector y preceptor. Si se presentan 5 personas para el  primer cargo, 4 para el segundo y 15 para el tercero; ¿de cuántas maneras pueden seleccionarse?.

5) Hallar n

a) C_n,2 -15 = 0          b) V_n,2 = 12

6) Desarrollar utilizando la fórmula del binomio

a) (x+4)⁷           b) [(x/2)+y]⁴

7) Hallar el término 20 del desarrollo (a+a²)²³

8) Hallar x en (-2x-1)¹⁰ si el término central vale  - 8064

9) Que lugar ocupa el término en w³⁰ del desarrollo (w²+3y)¹⁹

10) Hallar k en el desarrollo (1+k)⁷  si el producto entre el primer y segundo término es -1   

Vectores

1)  Dado los vectores u=(4,2)  v=(-1,3) y w=(5,-2) calcular

a) u+v-w   b) 3v-2u+w     c) mod u   (módulo de u)     d) mod(w-v)

2) Hallar el versor asociado a  z=(1,-1,2)

3) Hallar el vector v tal que (2,-3,1)=3(-1,2,0)+2v+5(2,-1,1)

4) Hallar la distancia entre los vectores a=(1,2,-1)  b=(3,4,-2)

5) Hallar k para que los vectores sean ortogonales, siendo u=(2,k,-1) y  v=(-4,3,5)

6) Hallar un vector v de dimensión 2, ortogonal a w=(3,-2) tal que la norma (módulo) es 117^1/2

7) Determinar si los siguientes vectores son linealmente independientes

a= (1,1,2)     b=(-1,-1,3)      c=(0,2,-1)

8) Determinar si v=(4,2) es combinación lineal de a=(2,1) y b=(-1,5)

Matrices

1) Determinar si las matriz P es combinación lineal de Q y S, donde

2) Hallar el vector   columna  C  tal que A.C=5C   si       

3) Calcular A² + 2A - 4I   si  

4) Investigar el rango de la matriz  A=C.E  donde  

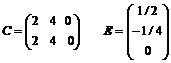
5) Verificar si  

6) Del ejercicio anterior, determinar si es válida la igualdad 

Determinantes

1) Hallar k tal que

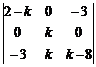
2) Hallar k, para que la matriz sea inversible

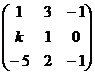
3) Hallar k tal que  

4) Resolver

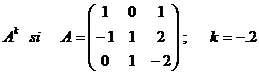
5) Hallar X en AX=B si  

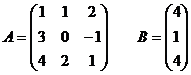
6) Hallar los valores de λ tales que

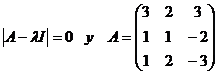
Sistema de ecuaciones  e inecuaciones

1) Estudiar la compatibilidad y resolver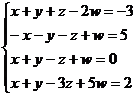

2) El siguiente sistema no es lineal; aplique un cambio de variable para resolverlo

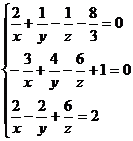
3) Resolver

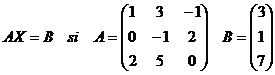
4) Resolver

5) Que condición debe cumplir a, b y c  para que el sistema homogéneo presente infinitas soluciones.

6) Determine las matrices A y B tales que

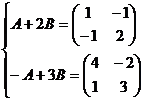
7) Dadas las siguientes funciones, determine cual es la oferta y la demanda. Encuentre el punto de equilibrio.  

8) Dada la matriz insumo producto correspondiente a dos industrias,  hallar la producción total de cada sector para una demanda final de 30 para la primer industria y 60 para la segunda

9) Determine si existe el conjunto solución correspondiente la sistema de inecuaciones

10) Dado el sistema de inecuaciones, encuentre la solución y maximice según la función f(x,y)